高正祺,本次论文的第一作者,先后于 2018和2021年在复旦大学微电子学院取得本科和硕士学位,现于麻省理工学院电子工程与计算机科学系(MIT EECS)攻读博士学位,师从Prof. Duane Boning,其目前主要研究方向为光子集成电路的设计自动化。
论文通讯作者为Dr.Ron Rohrer,现为美国南卫理公会大学电子与计算工程系(SMU ECE)教授,美国工程院院士,IEEE life fellow,TCAD的创刊人;其主要研究方向为电路理论。
集成电路中的良率估计问题(yield estimation)在近二十年一直是一个热点问题。狭义上的良率特指参数良率(parametric yield),即由于工艺波动带来的芯片失效。具体地说,在流片时由于工艺波动(process variation)的影响,实际生产出的器件可能偏离了设计中给定的数值。这种现象会导致生产出的100个芯片中,只有一部分达到了性能指标的要求;这部分满足性能指标的芯片占全部芯片的比例通常被称为良率。为了让设计者在设计时清楚地了解工艺波动的大小,工艺厂商通常会提供PDK文件给设计者。在PDK文件中不仅会定义本工艺下所使用器件的电流电压特性,还会定义随机变量来描述器件的工艺波动。
蒙特卡洛方法(Monte Carlo method)是最简单直接的一种良率估计方法。首先我们根据PDK文件对自己设计的电路产生N个样本,对每一个样本进行一次仿真并且检查其是否满足设计指标。最后的良率估计值为Nsuc/N,其中Nsuc为满足设计指标的样本个数。蒙特卡洛方法需要大量的样本来得到一个准确的良率估计。值得一提的另外一个相关概念是失效率(failure rate)。与良率不同,失效率指代所设计电路不能正常工作的概率;特别的,对于一个给定的电路,良率和失效率满足公式:良率 + 失效率 = 100%。文献中定义失效率是为了更方便地描述含有数百万甚至数十亿个重复单元的大规模电路(如随机静态存储器SRAM)。具体地说,例如为了保证1Mb的随机静态存储器阵列能够稳定地正常工作,每一个位单元的良率要大于99.999999% [1];在这种情况下,学者们发现使用失效率去分析是更为方便的。由于篇幅限制,本文末的参考文献部分只列举了部分工作[1]-[25];感兴趣的读者可以翻阅这些文献以及他们所引用的文献。
本文主要介绍发表在IEEE TCAD上题为“Efficient Non-Monte-Carlo Yield Analysis based on Adjoint Circuit Sensitivity”的一篇论文。这篇论文提出了一种 基于伴随方法(adjoint method)的非蒙特卡洛良率估计方法;其只需两次仿真就可以估计电路的良率数值。伴随方法基于特勒根定理(Tellegen’s theorem),可以快速估计梯度数值。作为例子,我们考虑图1(a)中的一个纯电阻电路,假定我们现在想要求v2关于R1(或者R2)的导数。我们先在图1(b)中绘制出图1(a)的伴随电路(adjoint circuit)。根据传统,伴随电路中的电压和电流通常使用φ(psi)和Ф(phi)来表示。关于如何构建伴随电路,感兴趣的读者可以翻阅文末参考文献[26]-[27]。对原始电路和伴随电路使用特勒跟定理,我们有:
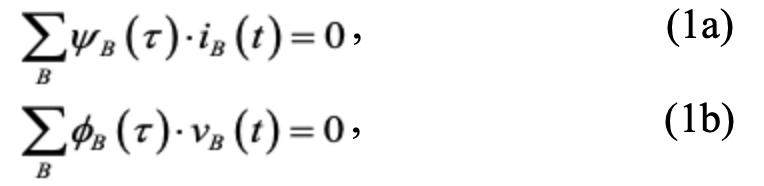
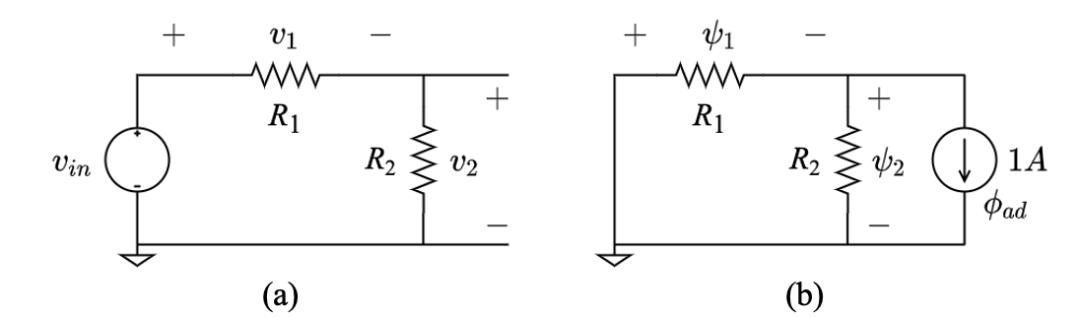
图1. (a)原始电路, (b)伴随电路
这里的求和是关于所有的分支(branch)。假定我们分别对原始电路中的分支电流和分支端口电压添加一个小的扰动δiB和δvB(这里小的扰动可以理解成由于R1和R2的数值发生了波动所导致的,类比真正集成电路中的工艺波动)。对扰动后的原始电路和伴随电路再次使用特勒跟定理,我们得到:
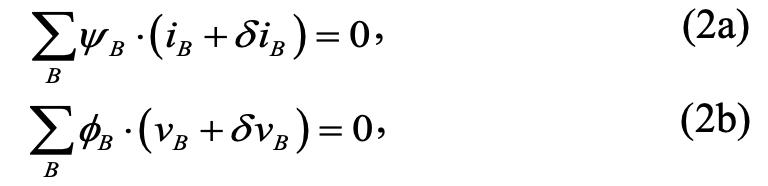
公式(2a)减去(1a);公式(2b)减去(1b)。并且把得到的两个表达式整合到一起,我们得到:

注意到图1中电路只含有两类支路:(i)电源支路(用S表示),(ii)电阻支路(用R表示)。我们将上面表达式按照支路的特征展开,并且将电阻支路移到表达式另一侧:
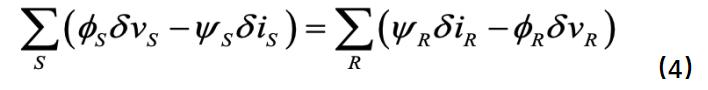
对于电阻支路,我们有:
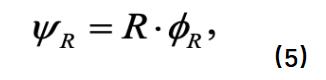
这是由于若原始电路中为电阻支路,则伴随电路中也为电阻支路,电阻值不变并且满足欧姆定律。同样的我们对原始电路的电阻支路列出欧姆定律,并且利用微分公式:
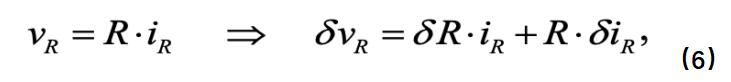
将公式(5)和(6)带入公式(4),化简得到:
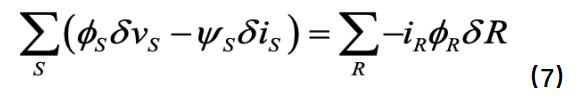
按照图1将公式(7)的左侧展开,我们得到:
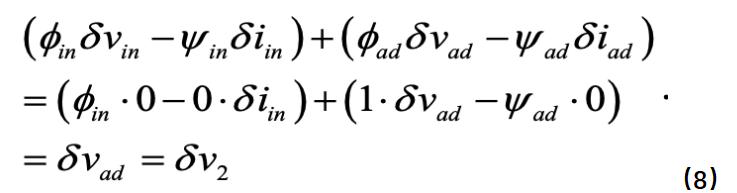
即公式(7)可以化简为:
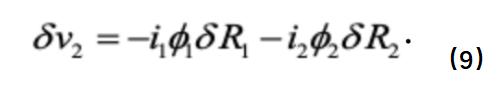
如果我们通过列出KCL和KVL求解出{i1, i2, Ф1, Ф2}并且带入回公式(9),我们得到:
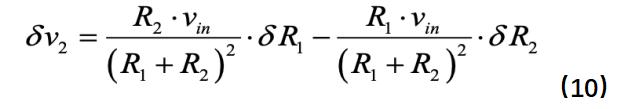
显然在δR1 和δR2前面的系数就是我们要求的导数∂v2/∂R1 和∂v2/∂R2。回忆上述过程,我们只需要求解原始电路和伴随电路,得到所有支路电流和电压,即可通过公式(9)得到导数值。在例子中,我们只考虑了v2对于{R1,R2}的导数。实际上,若我们想要求解{i1,i2,v1,v2}关于{R1,R2}的全部8个导数,运算时间并不会增加太多;这可以通过复用MNA方法构建的电路矩阵实现。对于含有电容电感和电阻的电路,我们可以在s域进行操作,即把(sC)-1和sL当作电阻。对于更复杂的同时还含有非线性元件的电路,我们可以使用反向欧拉法(back Euler method)对电路在每一个时间点上做近似,得到一个纯电阻电路;从而依旧可以使用伴随方法。这种基于伴随电路的导数求解方法,在电路元件很多时要比数值方法f(x+ε)-f(x)/ε快的多。粗略地说,通过伴随方法,仅需要两次仿真就可以计算得到电路中全部{i,v}对任意元件的导数。
有了这些导数,求解良率便是很简单的。我们需要的就是一阶泰勒展开和一点点统计知识。首先,我们对电路性能y=f(x)在其设计目标值y*=f(x*)处进行泰勒展开:
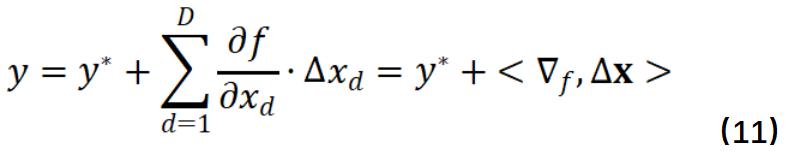
这里▽f表示梯度向量,可以通过前述的伴随方法计算得到。这里Δx=x-x*表示工艺波动,且其服从一个高维高斯分布:

根据统计知识以及泰勒展开的表达式,我们知道y也服从一个高斯分布且均值和方差都可以计算得到:
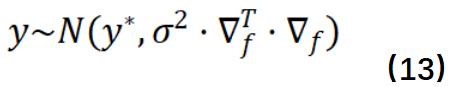
现在我们已经有了电路性能y的分布,那么良率就是一个关于高斯分布的积分:
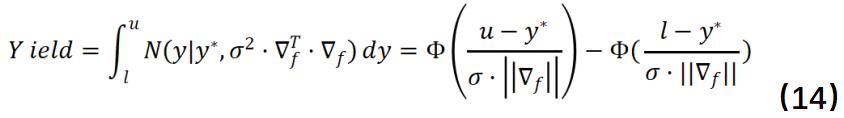
Ф表示标准高斯分布的累积分布函数(cumulative distribution function)。[l,u]表示电路性能的范围。如果有多个想要考虑的电路性能, 那么最后我们将得到一个关于高维高斯分布的积分,虽然没有闭式解,但由于高斯分布已知,我们可以通过采样方法来近似估计这一概率数值;在现代计算机上,这一步骤几秒便可以完成。论文展示了几个例子,并且和之前的一个非蒙特卡洛的方法做了对比。
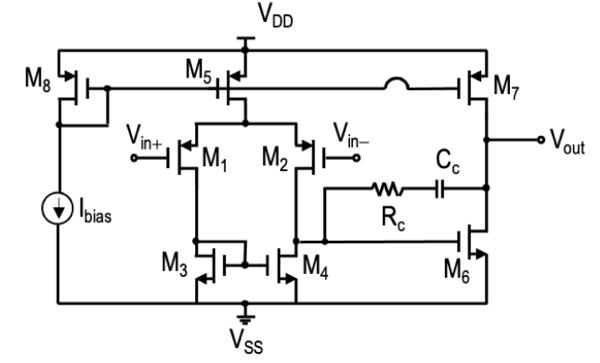
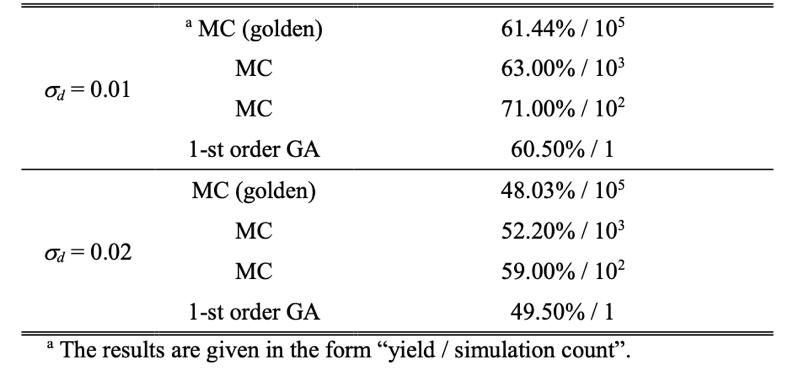
图2. 一个OPAMP例子以及其对应的实验结果
除了良率估计的方法,该论文还提出了一种分析哪个器件对良率影响最大的方法。其核心思想是利用贪婪算法以及韦恩图对所有的器件波动进行一遍快速遍历,按照影响良率的程度进行从大到小的排序。
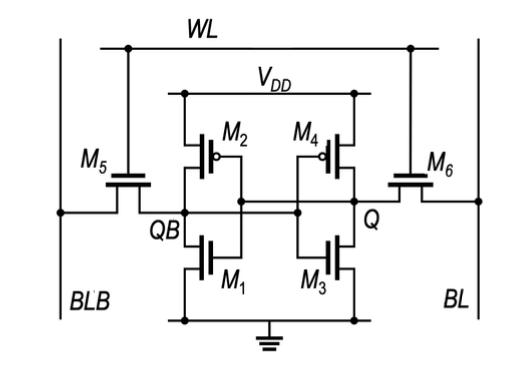

图3. SRAM的一个单元电路示意图,蓝色线表示器件对良率的影响按照从小到大排列
来源:芯系清华
作者:高正祺

欢迎各公众号,媒体转载
投稿/推广/合作/入群/赞助/转发 请加微信13488683602
