е…іжіЁ+жҳҹж Үе…¬дј—еҸ·пјҢдёҚй”ҷиҝҮзІҫеҪ©еҶ…е®№
иҪ¬иҮӘ | е°ҸйәҰеӨ§еҸ”
еҒҡиҝҮиҝҗеҠЁжҺ§еҲ¶зҡ„е°ҸдјҷдјҙйғҪзҹҘйҒ“пјҢSжӣІзәҝеҫҲйҮҚиҰҒпјҢдёӢйқўдёҖеј еҠЁеӣҫеҜ№жҜ”дёҖдёӢпјҢдҪ е°ұзҹҘйҒ“SжӣІзәҝзҡ„еҘҪеӨ„пјҡ
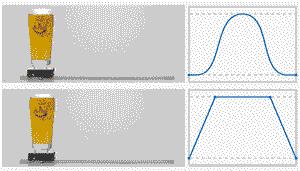
дёӢйқўеҲҶдә«дёҖдёӢSжӣІзәҝзҡ„еҶ…е®№пјҡ
1 еүҚиЁҖ
SеҪўеҠ еҮҸйҖҹзҡ„жңҖйҮҚиҰҒзү№еҫҒжҳҜиҜҘз®—жі•зҡ„еҠ йҖҹеәҰ/еҮҸйҖҹеәҰжӣІзәҝзҡ„еҪўзҠ¶еҰӮеӯ—жҜҚ SгҖӮSеҪўеҠ еҮҸйҖҹзҡ„йҖҹеәҰжӣІзәҝе№іж»‘ ,д»ҺиҖҢиғҪеӨҹеҮҸе°‘еҜ№жҺ§еҲ¶иҝҮзЁӢдёӯзҡ„еҶІеҮ»пјҢ并дҪҝжҸ’иЎҘиҝҮзЁӢе…·жңүжҹ”жҖ§ [^1]гҖӮз”ұдәҺTеҪўжӣІзәҝеңЁеҠ йҖҹеҲ°еҢҖйҖҹзҡ„еҲҮжҚўиҝҮзЁӢдёӯпјҢе®һйҷ…дёӯеӯҳеңЁиҫғеӨ§иҝҮеҶІпјҢеӣ жӯӨиҝҷйҮҢеҜ№жҜ”дёҖдёӢTжӣІзәҝе’Ң7ж®өSжӣІзәҝзҡ„е®һйҷ…иҝҮзЁӢпјӣ
- TеҪўпјҡеҠ йҖҹ -> еҢҖйҖҹ -> еҮҸйҖҹ
- SеҪўпјҡеҠ еҠ йҖҹ() -> еҢҖеҠ йҖҹ() -> еҮҸеҠ йҖҹ()-> еҢҖйҖҹ()-> еҠ еҮҸйҖҹ()-> еҢҖеҮҸйҖҹ()-> еҮҸеҮҸйҖҹ()
дёҠж–ҮеңЁеҠ йҖҹиҝҷеқ—зҡ„ж–Үеӯ—жҸҸиҝ°еҸҜиғҪиҜ»иө·жқҘиө·жқҘжңүзӮ№з»•пјҢдёӢйқўзңӢеӣҫпјҡ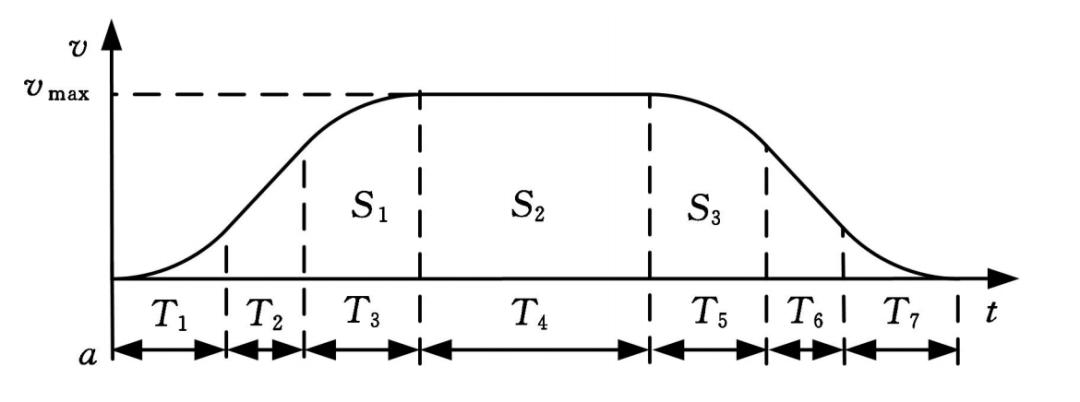
2 зҗҶи®әеҲҶжһҗ
з”ұдәҺSжӣІзәҝеңЁеҠ еҮҸйҖҹзҡ„иҝҮзЁӢдёӯпјҢе…¶еҠ йҖҹеәҰжҳҜеҸҳеҢ–зҡ„пјҢеӣ жӯӨиҝҷйҮҢеј•е…ҘдәҶж–°зҡ„дёҖдёӘеҸҳйҮҸ пјҢеҚіеҠ еҠ йҖҹеәҰгҖӮ
еӣ жӯӨеҜ№еә”дёҠеӣҫзҡ„7ж®өSйҖҹеәҰжӣІзәҝдёӯпјҢ规е®ҡжңҖеӨ§еҠ йҖҹдёәпјҢжңҖе°ҸеҠ йҖҹеәҰдёәпјҢеҲҷеҠ йҖҹеәҰзҡ„е…ізі»пјӣ
- еҠ еҠ йҖҹ()пјҡйҖҗжёҗеўһеӨ§пјӣ
- жӯӨж—¶
- еҢҖеҠ йҖҹ()пјҡиҫҫеҲ°жңҖеӨ§пјӣ
- жӯӨж—¶
- еҮҸеҠ йҖҹ()пјҡйҖҗжёҗеҮҸе°Ҹпјӣ
- жӯӨж—¶
- еҢҖйҖҹ()пјҡдёҚеҸҳеҢ–пјӣ
- жӯӨж—¶
- еҠ еҮҸйҖҹ()пјҡ йҖҗжёҗеўһеӨ§пјӣ
- жӯӨж—¶
- еҢҖеҮҸйҖҹ()пјҡ иҫҫеҲ°жңҖеӨ§пјӣ
- жӯӨж—¶
- еҮҸеҮҸйҖҹ()пјҡ йҖҗжёҗеҮҸе°Ҹпјӣ
- жӯӨж—¶
дёәеҠ йҖҹеәҰзҡ„з»қеҜ№еҖјпјӣе…¶дёӯ
жүҖд»ҘйҖҡеёёйңҖиҰҒзЎ®е®ҡдёүдёӘжңҖеҹәжң¬зҡ„зі»з»ҹеҸӮж•° :зі»з»ҹжңҖеӨ§йҖҹеәҰ пјҢжңҖеӨ§еҠ йҖҹеәҰa_{max} пјҢеҠ еҠ йҖҹеәҰпјҢе°ұеҸҜд»ҘеҸҜзЎ®е®ҡж•ҙдёӘиҝҗиЎҢиҝҮзЁӢ[^2] пјӣ
- жңҖеӨ§йҖҹеәҰпјҡеҸҚжҳ дәҶзі»з»ҹзҡ„жңҖеӨ§иҝҗиЎҢиғҪеҠӣ пјӣ
- жңҖеӨ§еҠ йҖҹеәҰпјҡеҸҚжҳ дәҶзі»з»ҹзҡ„жңҖеӨ§еҠ еҮҸйҖҹиғҪеҠӣ пјӣ
- еҠ еҠ йҖҹеәҰпјҡеҸҚжҳ дәҶзі»з»ҹзҡ„жҹ”жҖ§пјӣ
- жҹ”жҖ§и¶ҠеӨ§пјҢиҝҮеҶІи¶ҠеӨ§пјҢиҝҗиЎҢж—¶й—ҙи¶Ҡзҹӯпјӣ
- жҹ”жҖ§и¶Ҡе°ҸпјҢиҝҮеҶІи¶Ҡе°ҸпјҢиҝҗиЎҢж—¶й—ҙи¶Ҡй•ҝпјӣ
2.1 еҠ йҖҹеәҰж—¶й—ҙе…ізі»ж–№зЁӢ
ж•ҙдёӘеҠ йҖҹеәҰеҸҳеҢ–зҡ„иҝҮзЁӢе…·дҪ“еҰӮдёӢеӣҫжүҖзӨәпјӣ
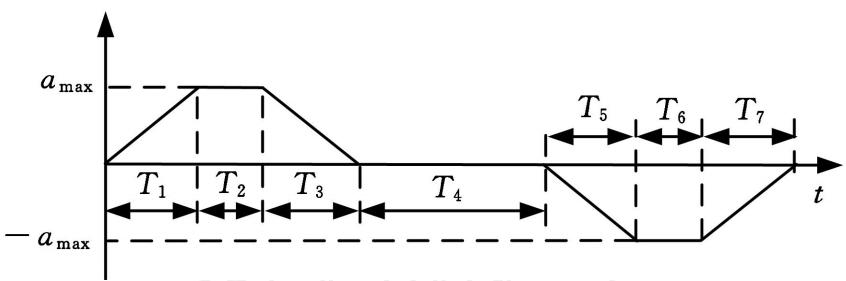
еҶҚж¬Ўејәи°ғдёҖдёӢ е’Ң зҡ„е…ізі»пјҢеҸҰеӨ–иҝҷйҮҢеҶҚеј•е…ҘеҸҳйҮҸ пјҢ
в‘жҜ”еҰӮпјҢеҪ“еүҚж—¶еҲ» ,еҚі дҪҚдәҺеҢәй—ҙ пјҢеҲҷеҰӮжһңе°Ҷ дҪңдёәеҲқе§ӢзӮ№пјҢеҲҷ дёә зӣёеҜ№дәҺж—¶еҲ»зҡ„ж—¶й—ҙпјҢеҲҷжңүпјҡ
дёӢйқўеҸҜд»Ҙеҫ—еҲ°еҠ йҖҹеәҰдёҺж—¶й—ҙзҡ„е…ізі»еҮҪж•°пјҢе…·дҪ“еҰӮдёӢпјҡ
ж №жҚ® в‘ ејҸпјҢе°Ҷ д»Је…Ҙ в‘Ў ејҸеҸҜд»Ҙеҫ—еҲ°пјҡ
дёҠејҸдёӯ пјӣ
2.2 йҖҹеәҰж—¶й—ҙе…ізі»ж–№зЁӢ
йҖҹеәҰе’ҢеҠ йҖҹеәҰж»Ўи¶і пјӣеҠ еҠ йҖҹеәҰе’ҢйҖҹеәҰзҡ„е…ізі»ж»Ўи¶іпјҡ
з»“еҗҲеҠ йҖҹеәҰж—¶й—ҙ关系并结еҗҲв‘Ў ејҸеҸҜд»Ҙеҫ—еҲ°йҖҹеәҰжӣІзәҝе…ізі»пјҢе…·дҪ“е…ізі»еҰӮдёӢеӣҫжүҖзӨәпјӣ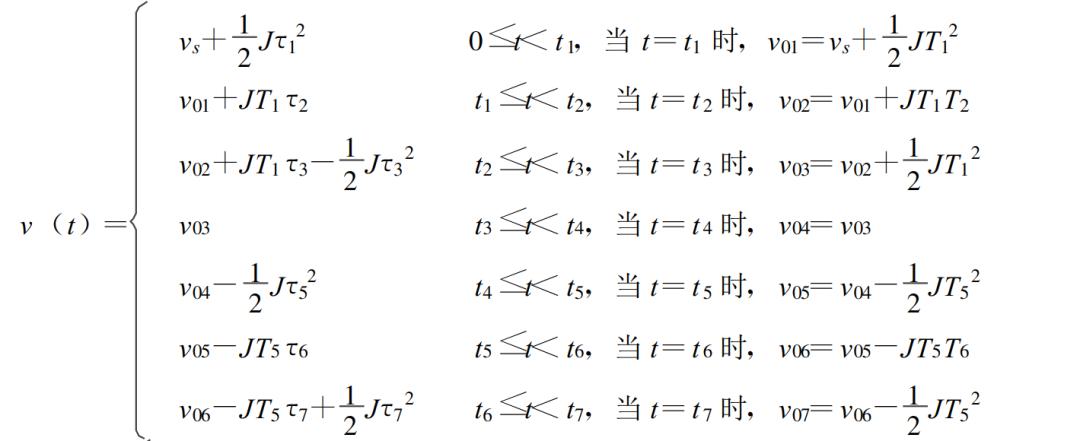
иҝӣдёҖжӯҘз®ҖеҢ–еҸҜд»Ҙеҫ—еҲ°пјҡ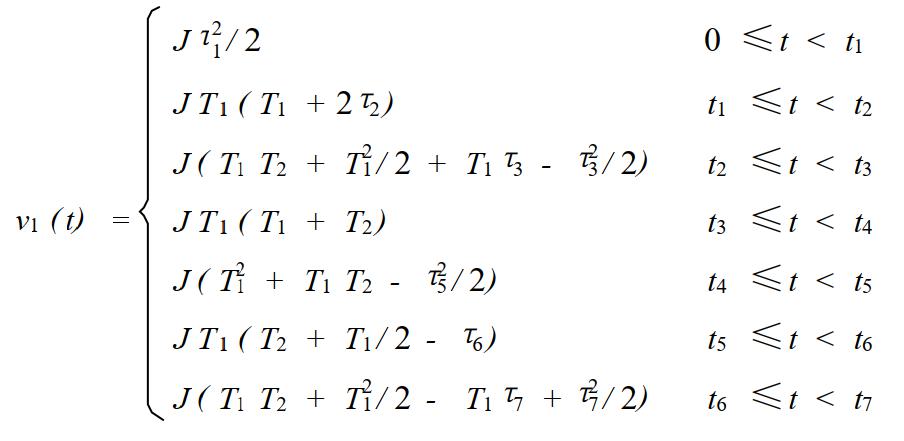
2.3 дҪҚ移时й—ҙе…ізі»ж–№зЁӢ
дҪҚ移 е’ҢеҠ еҠ йҖҹеәҰ зӣҙжҺҘж»Ўи¶іе…ізі»еҰӮдёӢпјҡ
з®ҖеҚ•жҺЁеҜј
еӣ жӯӨеҸҜд»Ҙеҫ—еҲ°пјҡ
вҖңз§ҜеҲҶеҝҳзҡ„е·®дёҚеӨҡдәҶпјҢеӣһеҺ»еҶҚеӨҚд№ дёҖдёӢпјӣ
жңҖз»ҲдҪҚ移зҡ„ж–№зЁӢеҰӮдёӢжүҖзӨәпјӣ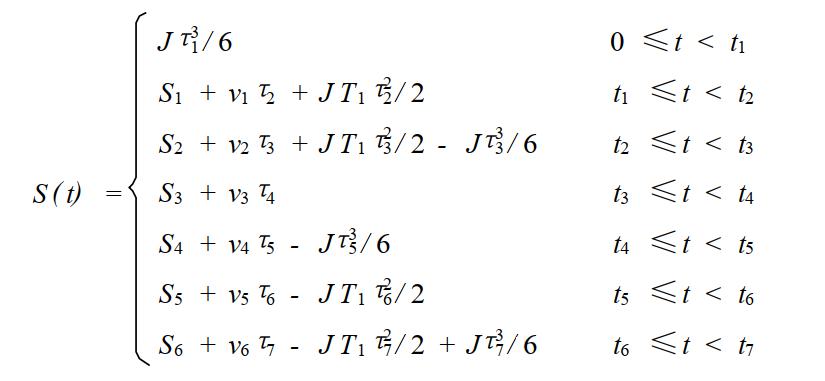
3 зЁӢеәҸе®һзҺ°зҡ„жҖқи·Ҝ
жӯЈеҰӮеүҚйқўжүҖжҸҗеҲ°зҡ„пјҢSжӣІзәҝ规еҲ’йңҖиҰҒзЎ®е®ҡдёүдёӘжңҖеҹәжң¬зҡ„зі»з»ҹеҸӮж•° пјҡзі»з»ҹжңҖеӨ§йҖҹеәҰ пјҢжңҖеӨ§еҠ йҖҹеәҰa_{max} пјҢеҠ еҠ йҖҹеәҰпјҢиҝҷж ·е°ұеҸҜд»ҘзЎ®е®ҡиҝҷдёӘиҝҗиЎҢиҝҮзЁӢгҖӮиҝҷйҮҢжңүдёҖдёӘйҡҗжҖ§зҡ„жқЎд»¶пјҢе°ұжҳҜеңЁиҝҗиЎҢзҡ„иҝҮзЁӢдёӯеҸҜд»ҘиҫҫеҲ°жңҖеӨ§йҖҹеәҰпјҢиҝҷж ·жүҚжҳҜе®Ңж•ҙзҡ„7ж®өSжӣІзәҝпјҢеҸҰеӨ–иҝҷйҮҢиҝҳжңүдёҖдәӣдёӯй—ҙеҸӮж•°пјҡ
- пјҢеӣ жӯӨжңү пјӣ
- еҠ еҠ йҖҹеәҰ пјӣ
- пјӣ
- пјҢз”ЁжҲ·з»ҷе®ҡж•ҙдёӘиҝҗиЎҢиҝҮзЁӢжүҖйңҖиҰҒзҡ„ж—¶й—ҙпјӣ
дҪҶжҳҜйҖҡеёёе®һйҷ…иҝҮзЁӢдёӯе…іеҝғпјҢпјҢпјӣ
3.1 жҺЁеҜј
зҗҶжғізҠ¶жҖҒеҒҮи®ҫеӯҳеңЁ е’ҢпјҢеҲҷжҺЁеҜјиҝҮзЁӢеҰӮдёӢпјҡ
еӣ жӯӨеҸҜд»Ҙеҫ—еҲ°пјҡ
з®ҖеҢ–д№ӢеҗҺеҫ—еҲ°пјҡ
ж №жҚ®в‘ЎејҸеҸҜзҹҘпјҡ
жңҖз»Ҳеҫ—еҲ°пјҡ
вҖңдёәеҲқе§ӢйҖҹеәҰпјӣ
дёӢйқўеҸҜд»Ҙж №жҚ®дҪҚ移时й—ҙе…ізі»ж–№зЁӢиҝӣиЎҢзҰ»ж•ЈеҢ–зҡ„зЁӢеәҸзј–еҶҷгҖӮ
еҒҮи®ҫеҸҜд»ҘеҲ°иҫҫжңҖеӨ§йҖҹеәҰпјҢдё”з”ЁжҲ·з»ҷе®ҡдәҶж•ҙдёӘиҝҮзЁӢиҝҗиЎҢж—¶й—ҙпјҢеҲҷ зҡ„жҺЁеҜјеҰӮдёӢпјҡ
з®ҖеҢ–дёҠејҸеҸҜд»Ҙеҫ—еҲ°пјҡ
ж №жҚ® д»Је…ҘдёҠејҸеҸҜеҫ—пјҡ
3.2 зҡ„жҺЁеҜј
иҝҷж—¶еҖҷиҝҳеү©дёӢйңҖиҰҒи®Ўз®—пјҢйҖҡиҝҮе·ІйҮҸ еҸҜд»ҘжҺЁеҜјеҮәжқҘпјӣйҰ–е…ҲдҪҚ移д№Ӣй—ҙж»Ўи¶іе…ізі»еҰӮдёӢпјҡ
е…¶дёӯеҠ йҖҹеҢәй•ҝеәҰдёә пјӣе…¶дёӯеҮҸйҖҹеҢәй•ҝеәҰдёә пјӣ
е…·дҪ“жҺЁеҜјпјӣ[^2] еүҚйқўжҸҗеҲ°иҝҮпјҢпјҢеӣ жӯӨеңЁ=0зҡ„ж—¶еҖҷпјҢеҲҷ
иҝҷйҮҢз®ҖеҚ•жҺЁеҜјдёҖдёӢпјҡ
ж №жҚ®в‘ЈпјҢв‘ӨжңҖз»Ҳз®ҖеҢ–еҫ—еҲ°пјҡ
вҖңпјҡдёәиҝҗиЎҢзҡ„жҖ»ж—¶й—ҙпјҡдёәиҝҗиЎҢзҡ„жҖ»и·ҜзЁӢ
иҜҰз»ҶжҺЁеҜјиҝҮзЁӢеҰӮдёӢпјҡ
еӣ дёәпјҡ
еӣ дёәпјҡ
жүҖд»ҘпјҢз®ҖеҢ–еҫ—еҲ°пјҡ
жүҖд»ҘеҸҜд»Ҙеҫ—еҲ°пјҡ
еӣ дёәпјҡ
е°Ҷе…¶д»Је…ҘеҸҜд»Ҙеҫ—еҲ°пјҡ
з®ҖеҢ–еҫ—еҲ°жңҖз»Ҳз»“жһңпјҡ
4 matlab зЁӢеәҸ
matlabзЁӢеәҸдәІжөӢеҸҜд»ҘиҝҗиЎҢпјҢеҒҡдәҶз®ҖеҚ•зҡ„дҝ®ж”№пјҢ
еӣ дёәиҝҷйҮҢзӣҙжҺҘз»ҷе®ҡдәҶж•ҙдёӘиҝҗиЎҢиҝҮзЁӢзҡ„ж—¶й—ҙпјҢжүҖд»ҘйңҖиҰҒеңЁSCurveParaеҮҪж•°дёӯжұӮеҮәеҠ еҠ йҖҹеәҰ зҡ„еҖјпјҢи·ҜзЁӢдёә 1пјҡ
SCurvePara
function [Tf1,V,A,J,T] = SCurvePara(Tf, v, a)
T = zeros(1,7);
for i=1:1000
% еҠ еҠ йҖҹеәҰ J
J = (a^2 * v) / (Tf*v*a - v^2 - a);
% Tk
T(1) = a / J;
T(2) = v / a - a / J; % t2 = v / a - t1;
T(3) = T(1);
T(4) = Tf - 2 * a / J - 2 * v / a; % t4 = Tf - 4*t1 - 2*t2;
T(5) = T(3);
T(6) = T(2);
T(7) = T(1);
% ж №жҚ®T2е’ҢT4еҲӨж–ӯSжӣІзәҝзҡ„зұ»еһӢ
if T(2) < -1e-6
a = sqrt(v*J);
display('t2<0');
elseif T(4) < -1e-6
v = Tf*a/2 - a*a/J;
display('t4<0');
elseif J < -1e-6
Tf = (v^2 + a) / (v*a) + 1e-1;
display('J<0');
else
break;
end
end
A = a;
V = v;
Tf1 = Tf;
end
SCurveScaling
function s = SCurveScaling(t,V,A,J,T,Tf)
% J = (A^2 * V) / (Tf*V*A - V^2 - A);
% T(1) = A / J;
% T(2) = V / A - A / J; % T(2) = V / A - T(1);
% T(3) = T(1);
% T(4) = Tf - 2 * A / J - 2 * V / A; % T(4) = Tf - 4*T(1) - 2*T(2);
% T(5) = T(3);
% T(6) = T(2);
% T(7) = T(1);
%%
if (t >= 0 && t <= T(1))
s = 1/6 * J * t^3;
elseif ( t > T(1) && t <= T(1)+T(2) )
dt = t - T(1);
s = 1/2 * A * dt^2 + A^2/(2*J) * dt...
+ A^3/(6*J^2);
elseif ( t > T(1)+T(2) && t <= T(1)+T(2)+T(3) )
dt = t - T(1) - T(2);
s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
+ 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3) && t <= T(1)+T(2)+T(3)+T(4) )
dt = t - T(1) - T(2) - T(3);
s = V*dt ...
+ (-1/6*J*T(3)^3) + 1/2*A*T(3)^2 + (A*T(2) + A^2/(2*J))*T(3) + 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
elseif ( t > T(1)+T(2)+T(3)+T(4) && t <= T(1)+T(2)+T(3)+T(4)+T(5) )
t_temp = Tf - t;
dt = t_temp - T(1) - T(2);
s = -1/6*J*dt^3 + 1/2*A*dt^2 + (A*T(2) + A^2/(2*J))*dt ...
+ 1/2*A*T(2)^2 + A^2/(2*J)*T(2) + A^3/(6*J^2);
s = 1 - s;
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6) )
t_temp = Tf - t;
dt = t_temp - T(1);
s = 1/2 * A * dt^2 + A^2/(2*J) * dt + A^3/(6*J^2);
s = 1 - s;
elseif ( t > T(1)+T(2)+T(3)+T(4)+T(5)+T(6) && t <= T(1)+T(2)+T(3)+T(4)+T(5)+T(6)+T(7) + 1e5 )
t_temp = Tf - t;
s = 1/6 * J * t_temp^3;
s = 1 - s;
end
end
жөӢиҜ•зҡ„д»Јз ҒеҰӮдёӢпјҡTEST
%%
N = 500;
ThetaStart = 0; %иө·е§ӢдҪҚзҪ®
ThetaEnd = 90; %жңҖз»ҲдҪҚзҪ®
VTheta = 90; %1 йҖҹеәҰ
ATheta = 135; %1.5 еҠ йҖҹеәҰ
Tf = 1.8; % жҖ»иЎҢзЁӢж—¶й—ҙ
v = VTheta/(ThetaEnd - ThetaStart);
a = ATheta/(ThetaEnd - ThetaStart);
v = abs(v);
a = abs(a);
Theta = zeros(1,N);
s = zeros(1,N);
sd = zeros(1,N);
sdd = zeros(1,N);
[TF,V,A,J,T] = SCurvePara(Tf, v, a);
display(J, 'J:');
display(TF,'Tf:');
display(V,'v:');
display(A, 'da:');
display(TF-Tf,'dTf:');
display(V-v,'dv:');
display(A-a, 'da:');
t=linspace(0,TF,N);
dt = t(2) - t(1);
for i = 1:N
if i == N
a = a;
end
s(i) = SCurveScaling(t(i),V,A,J,T,TF);
Theta(i) = ThetaStart + s(i) * (ThetaEnd - ThetaStart);
if i>1
sd(i-1) = (s(i) - s(i-1)) / dt;
end
if i>2
sdd(i-2) = (sd(i-1) - sd(i-2)) / dt;
end
end
subplot(3,1,1);
legend('Theta');
xlabel('t');
subplot(3,1,1);
plot(t,s)
legend('дҪҚ移');
xlabel('t');
title('дҪҚзҪ®жӣІзәҝ');
subplot(3,1,2);
plot(t,sd);
legend('йҖҹеәҰ');
xlabel('t');
title('йҖҹеәҰжӣІзәҝ');
subplot(3,1,3);
plot(t,sdd);
legend('еҠ йҖҹеәҰ');
xlabel('t');
title('еҠ йҖҹеәҰжӣІзәҝ');
зңӢеҲ°жңҖз»Ҳд»ҝзңҹз»“жһңе’Ңйў„жңҹзӣёеҗҢпјӣ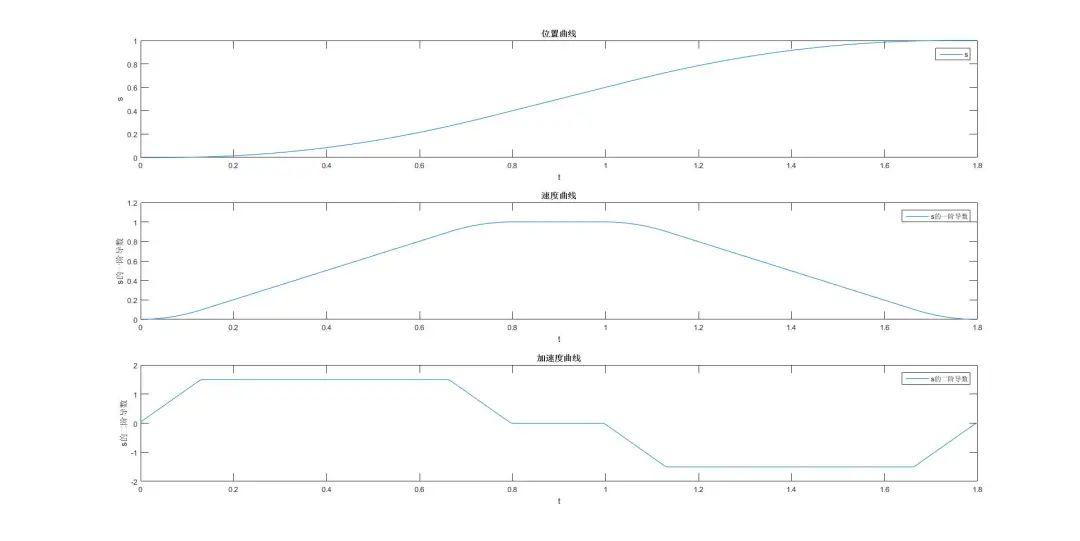
жңҖеҗҺеҶҚзңӢдёҖдёӢTеҪўе’ҢSеҪўйҖҹеәҰжӣІзәҝ规еҲ’зҡ„ж•ҲжһңеҜ№жҜ”пјҡ
5 жҖ»з»“
жң¬ж–ҮеҸӘеҜ№7ж®өзҡ„SжӣІзәҝ规еҲ’еҒҡдәҶиҜҰз»Ҷзҡ„жҺЁеҜје’Ңд»Ӣз»ҚпјҢmatlabдёӯзҡ„зЁӢеәҸеҜ№дәҺ4ж®өе’Ң5ж®өйғҪжңүеҒҡе®һзҺ°пјҢеҫҲеӨҡжҳҜеңЁзҗҶжғіжғ…еҶөдёӢиҝӣиЎҢжҺЁеҜјзҡ„пјҢеҲқе§ӢйҖҹеәҰй»ҳи®Өдёә0пјҢз»ҲжӯўйҖҹеәҰд№ҹдёә0пјҢ并且еҒҮи®ҫеҠ еҮҸйҖҹеҢәеҹҹзӣёдә’еҜ№з§°гҖӮжңҖз»ҲиҝҗиЎҢз»“жһңз¬ҰеҗҲйў„жңҹж•ҲжһңгҖӮ
вҖңж–Үдёӯйҡҫе…Қжңүй”ҷиҜҜе’Ңзә°жјҸд№ӢеӨ„пјҢиҜ·еӨ§дҪ¬д»¬дёҚеҗқиөҗж•ҷ
еҲӣдҪңдёҚжҳ“пјҢеҰӮжһңжң¬ж–Үеё®еҲ°дәҶжӮЁпјӣ
иҜ·её®еҝҷзӮ№дёӘиөһ ????????????пјӣ
иҜ·её®еҝҷзӮ№дёӘиөһ ????????????пјӣ
иҜ·её®еҝҷзӮ№дёӘиөһ ????????????пјӣ
6 еҸӮиҖғ
[^1]:йҷҲеҸӢдёң йӯҸжҙӘе…ҙ зҺӢзҗҰйӯҒ.ж•°жҺ§зі»з»ҹзҡ„зӣҙзәҝе’Ң S еҪўеҠ еҮҸйҖҹзҰ»ж•Јз®—жі•[D].еҢ—дә¬:дёӯеӣҪжңәжў°е·ҘзЁӢ,2010.
[^2]:йғӯж–°иҙө жқҺд»Һеҝғ S жӣІзәҝеҠ еҮҸйҖҹз®—жі•з ”з©¶ дёҠжө·дәӨйҖҡеӨ§еӯҰеӣҪ家模具 CAD е·ҘзЁӢз ”з©¶дёӯеҝғ , 200030
ж¬ўиҝҺе…іжіЁжҲ‘зҡ„е…¬дј—еҸ·пјҢеӣһеӨҚвҖңеҠ зҫӨвҖқжҢү规еҲҷеҠ е…ҘжҠҖжңҜдәӨжөҒзҫӨпјҢеӣһеӨҚвҖң1024вҖқжҹҘзңӢжӣҙеӨҡеҶ…е®№гҖӮ
ж¬ўиҝҺе…іжіЁжҲ‘зҡ„и§Ҷйў‘еҸ·пјҡ

зӮ№еҮ»вҖңйҳ…иҜ»еҺҹж–ҮвҖқжҹҘзңӢжӣҙеӨҡеҲҶдә«пјҢж¬ўиҝҺзӮ№еҲҶдә«гҖҒ收и—ҸгҖҒзӮ№иөһгҖҒеңЁзңӢгҖӮ
